Introduction to Trees

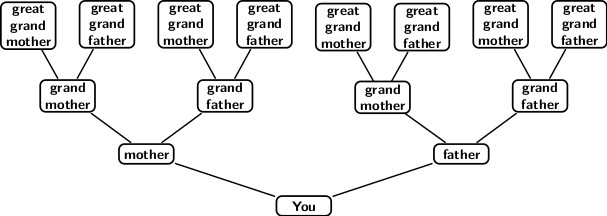
The terminology to describe trees is borrowed from the notion of a family tree. Ancestor-descendant relationships exist among the elements of a family tree. The oldest generation appears at the top of a family tree. Younger generations appear below older generation in the tree. Two successive generations are related by parent-child. Children and their parent are connected by links or branches. The picture of a family tree appears in the diagram below. The point from where family genealogy begins is called the root. For example, in the diagram above, you is the root.

A tree represents a hierarchic relationship among elements of data. Conventionally, unlike a family tree, a tree data structure is drawn bottom-up with the root at the top, and ancestor-descendants relationships are considered reversed. An
element of a tree is referred to as a node. It comprises of non-divisible data items to be processed as a unit with the link information to reach all the children and possibly the parent. We begin with the definition of a tree.

Definition: A tree T may be empty (null tree with no node), or may consist of

• A special node, designated as r, called the root.
• A set of k trees T₁, T₂, . . . , T_k (some could possibly empty) with roots r₁, r₂, . . . , r_k respectively.

T is constructed by making r₁, r₂, . . . , r_k as children of r. Trees T₁, T₂, . . . , T_k are called sub trees of T.

The above definition is recursive, as it defines a tree in terms of other trees.

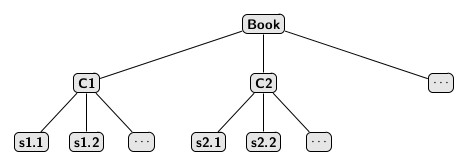
A hierarchy of chapters, sections, subsections and paragraphs of texts represents a book. We can denote the whole book as the root of the tree. Each chapter is a sub tree of the root. A chapter, in turn, represents a tree consisting of several sections, each of which is a sub tree of the chapter. The picture below provides the hierarchic relationships of a book, its chapters, sections, and subsections.

A tree is accessible through its root. Any processing of a tree requires a systematic traversal of the tree in which each node is accessed at least once. Storing a tree in a computer’s memory creates an automatic ordering of the siblings from the left to the right. In the relative ordering of a pair of siblings, one sibling appears to the other sibling. A node having no child is known as a leaf node while other nodes are called internal nodes.

If each node in a tree may have at most one sibling, then we call it a binary tree. Equivalently, in a binary tree, each node may have 0, 1 or two children. The two siblings of a parent p are known respectively as left child and right child of p. We will begin with binary tree in the next blog.

Back to Index