Traversal of Trees

The processing of information stored in a tree data structure requires each node of the tree to be accessed at least once. A tree is accessible only by its root node. However, as every node stores a pointer to its children, it is possible to access the children of a node when the latter is visited. Therefore, starting with the root, we can ccess all nodes of a tree by repeatedly following the children pointers from the node which has just been visited. The three systematic ways of traversing a tree are:

The output of a traversal procedure is a list of nodes ordered by their visit sequence. It is convenient to visualize the each traversals as a recursive procedure:

  1. For an empty tree, the empty sequence represents the preorder/postorder/inorder traversal list.
  2. If a tree consists of oonly the root node, then the root node represents the preorder/postorder/inorder traveral list.
  3. In general a tree T may be assumed to consist of a root r, and k subtrees T1, T2, ..., Tk.
    • Preorder traversal of T is the list obtained by the root concatenated with preorder traversal lists of T1, T2, ..., Tk.
    • Postorder traversal of T is the list obtained by the concatenation of postorder traversal lists of T1, T2, ..., Tk.
      • followed by the root.
    • Inorder traversal of T is the list obtained by the concatenation of inorder traversal list of T1 followed by the root then the inorder lists of subtrees T2, ..., and Tk.

Consider an example tree shown below to understand how the tree traversal procedures work.

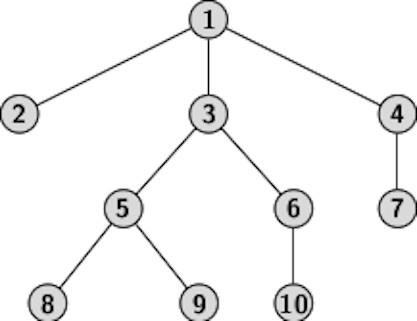
The preorder traversal list of the above tree is obtained by concatenating four lists, namely, {1} with the preorder traversal lists of three subtrees T2,T3, and T4. Using the recursive extension of preorder traversal to the three subtrees of the root, we obtain:

Therefore, the concatenating four lists {1} {3,5,8,9,6} {4,7} gives preorder traversal list of T as: 1,3,5,8,9,6,10,4,7. In the same manner we can obtain the postorder and the inorder traversal lists as:

Traversal is essentially a walk around the tree as shown in the figure below:

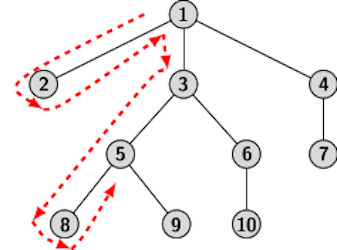
The walk starts from the root. Stying close to branches, we walk down in the direction shown in the figure. During the walk, each node is visited one more time than the number children it has. For example, we encounter a leaf node only once during a walk. However, the root node in the tree above, is encountered four times. Similarly, node 3 is visited four times:

The reader can find that the sequence we get from the walk around the tree is given by:

1(1) 2(1) 1(2) 3(1) 5(1) 8(1) 5(2) 9 (1) 5(3) 3(2) 6(1) 10(1)) 6(2)  3(3) 1(3) 4(1)7(1) 4(2) 1(4)

where subscript represent the instance of visiting a correspnding node. For example, node 1 is visited for the third instance when we walk along the tree from node 3 to node 4. We can now connect the walk around the tree in the context of three different traversals as follows.

The list of node visits for last instance is:

2(1) 8(1) 9(1) 5(3) 10(1) 6(2) 3(3) 7 (1) 4(2) 1(4)

Therefore, the postorder traversal sequence should be: 2 8 9 5 10 6 3 7 4 1

For binary trees k=2, we distinguish between two subtrees, the subtrees are referred to as the left subtree and the right subtree. The preorder, postorder and inorder traversals procedures are same as dicussed above but we can put them more compactly as follows:

For brevity, we denote the root as r, left subtree as L and right subtree as R. Using the notations, the preorder, postorder and inorder traversals procedures can be represented symbolically as rLR, LrR and LRr.

Back to Index