Shell Sort Algorithm
Shell sort uses a simple partitioning method over the given input sequence to gather and create logical subsequences. The mutual distance between adjacent elements in a sublist is a fixed interval. Initially, interval length is n/2, where n is the number of elements in the input. It requires log n passes of partitioning and sorting. We reduce the interval length of the partition by half in each pass. When the interval length is 0, we use compare-and-swap between adjacent pairs of elements to sort the array. Many researchers experimented with a different sequence of reducing interval lengths to explore shell sort’s efficiency. However, in our description we use conventional interval length starting with n/2.
In our description, we refer to the interval length between a pair of elements as gap g. For sorting the sublists, we use insertion sort. Let us represent the input sequence by arr[0], arr[1], …, arr[n-1]. Shell sort method is as follows:
- Start with g = ⌊n/2⌋</i> to defines sublists.
- Use insertion sort to sort the resulting subsequences
- Repeat partitioning and sorting with g = ⌊g/2⌋ until g > 0.
- Now, we compare and swap adjacent pairs of elements if necessary.
In particular, for the second pass g = n/4. So we have to carry out independent sorting of the following sub-sequences of the input
- The subsequence: {arr[0], arr[n/4], arr[n/2], arr[3n/4], a[n]}
- The subsequence: {arr[1], arr[(n/4)+1], arr[(n/2)+1], arr[(3n/4)+1]}
- The subsequence: {arr[2], arr[(n/4)+2], arr[(n/2)+2], arr[(3n/4)+2]}
- and so on.
In general, if we sort the subarrays consisting of elements at a gap of g then
- The subsequence: {arr[0], arr[g], arr[2g], arr[3g], …, arr[kg]}, where k = ⌊n/g⌋
- The subsequence: {arr[1], arr[g+1], arr[2g+1], arr[3g+1]. arr[kg+1]}
- The subsequence: {arr[2], arr[g+2], arr[2g+2], arr[3g+2]. arr[kg+2]}
- and so on.
After sorting all subsequences with gap g, we say the original sequence is g-sorted. In summary, the input is (n/2)-sorted, (n/4)-sorted, (n/8)-sorted, and so on. When it gets 0-sorted, then the sorting is complete. Let us understand the sorting process with an example. The figure below illustrates the process of defining subsequences and sorting them.
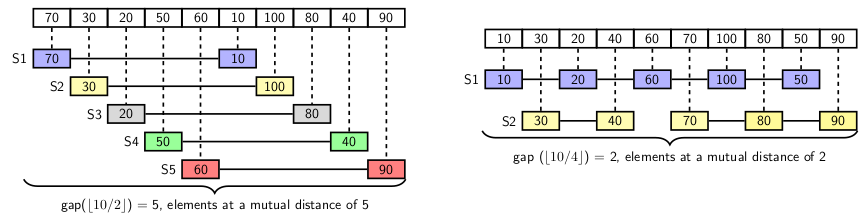
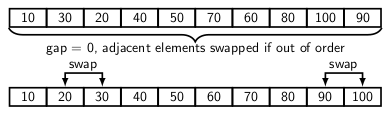
The input consists of 10 elements. We use a reducing interval sequence {5, 2, 1, 0} for creating the sublists. In the last pass, we 0-sort the sequence, which requires only two swaps. Notice that we do not physically create or partition to define the sublists. The procedure for sorting maintains the gap logically while sorting.
As far as time complexity is concerned, the number of passes is O(log n). Insertion sort takes worst-case time of O(n2. So, the worst-case time is computed as follows:
- Worst-case time for the last pass, i.e., sorting of elements 1-apart is n2
- Worst-case time for the pass before last, i.e., sorting of elements 2-apart is 2 * (n/2)2
- Worst-case time for sorting of elements 4-apart is 4 * (n/4)2
- and so on.
Therefore, the expression for time worst-case complexity is:
n2(1 + 1/2 + 1/22 + ...+ 1/2log (n-1)) = 2n2.
The best-case time occurs when the input is a sorted sequence. The best-case time is O(nlog n). The average case time for shell sort is the same as the best case. Experiments with different gap sequences indicate that the worst-case time for shell sort can be brought down to O(nlog n).