Deletion Operation on Red-Black Trees

A deletion operation in a red-black tree should handle two problems:

  1. Preserving BST property.
  2. Checking if any violation of color properties and restoring them.

The problem of preserving BST property without the complications of maintaining the color properties of a red-black tree is relatively simple. We discussed the complexities of deletion in BST earlier. For completeness, we briefly summarize the deletion rules for BST. The deletion of a node X from a BST depends on whether it is a leaf or an internal node. A quick recap of these rules appear below:

There are three cases for BST deletion:

  1. X’s is leaf node.
  2. X has only one child.
  3. X’s both children are nodes.

We did not consider external leaf nodes in BST. However, external nodes do not introduce any added complications. An external leaf node of a red-black tree is an external node with NULL pointers. A leaf node in a BST is mapped to a node having external nodes as its children in the corresponding red-black tree. We will refer to a BST leaf as an internal leaf in the red-black tree to distinguish it from an external leaf node.

The rules for the deletion of a node X in a BST are as follows:

  1. If X is a leaf node, delete it. It does not affect BST property of the tree after deletion.
  2. If X has one child Y, eliminate X and make the parent of X adopt Y as its child.
  3. If X has two children then first copy the value stored in the in-order successor, say Y, in X’s position then delete Y.

We have already proved that the in-order successor of node in a BST either has no children or has only one right child. Figure below illustrates rule 3 of a deletion in a BST,

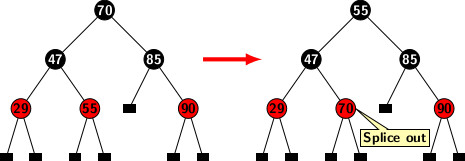
The little black rectangles in the figure represent external leaf nodes. The deletion of a node X may splice out a node at a position different from X unless X is a node with two external leaves. For example, to remove 70, we delete the node that had 55. However, it does not create any loss of information as the content of spliced node is copied in advance at the position where 70 was originally stored.

As indicated earlier, an external leaf node contains no information. All external leaf nodes are black. We will refer to an internal leaf simply as a leaf node. It is a node with two external leaves as children. A non-leaf red node cannot have one external leaf as one of its children as it violates the black height property of a legal red-black tree.

The rules for removing a node X depend on the position of the node spliced out from a red-black tree.

  1. If X is a red leaf then there is no problem. No color properties will be disturbed if X is deleted.
  2. If X is black and it has only one valid node Y as child, then Y must be red. Y replaces X and is recolored black.
  3. If X has two internal nodes as children, then the inorder successor node Y should be deleted.

Figure below illustrates deletion operations involving case 1 and case 2.


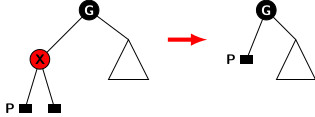
Case 1: Deletion of a red leaf


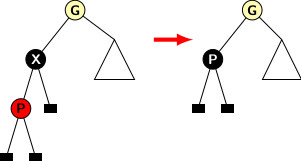
Case 2: Deletion of a black node with a single red child.

In case 3, if the inorder successor Y is a black leaf then we have to apply color compensation operations. Otherwise, either case 1 or case 2 should apply, and the deletion is done using the applicable rule.

The most complex instance of case 3 occurs when we attempt to delete a black leaf. It promotes an external leaf to occupy the position of the deleted node. The new external leaf acquires an excess black due to the removal of the black leaf as indicated in the figure below.


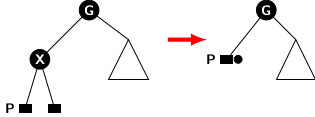
Case 3: Deletion of a black leaf node.

Removing a node X in a red-black tree promotes at least one node at a lower level. We shall refer to the node occupying the earlier position of X as the promoted node P, because it moves closer to the root. The color P as double black. The major issue in deletion is to handle the distribution of the extra black acquired by P. The figure below illustrates two situations stated above.

We need to consider a few structural conditions of the tree when a deletion occurs. In the following discussion, we denote the node acquiring excess black as v.

Case 3a: v’s sibling is black with a red child.

Figure below illustrates the two subcases

  1. when right child of s is red
  2. when left child of s is red.

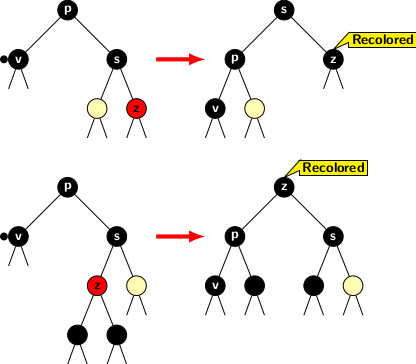
Handle the first subcase as follows.

The rotation operation promotes sibling s while recoloring red child increases the black height of the correspoinding subtree by 1. The other subtree of s is acquired by p. So the black height both subtrees of s are balanced. The excess black at v is
absorbed by the recolor of right child of s.

The readers can convince themselves that the recoloration followed by restructuring is correct for the second subcase. Two successive single rotations perform the restructuring of the tree: first a right rotation and then a left rotation around z. The first rotation bring z one level up and pushes s one level down. It may increase the black height of the right subtree of z after the first rotation. However, after second rotation z’s level is increases by 1 again and p is pushed one level down. Since z goes one level up, its right subtree also pushed one level up. So the original configuration of s and its two subtrees are restored. Recoloring z, it contributes 1 to the black heights of:

Therefore, we can remove the excess black of v as p also acquires the original left subtree of z.

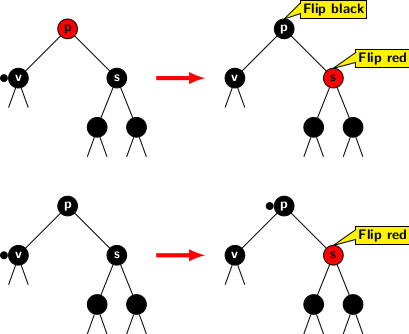
Case 3b: v’s sibling s is black and so are its children. Two subcases arise depend on the parent p’s color.

If p is red then exchanging colors of p and s we get rid of excess black from v. It adjusts the black height of p’s right subtree to the original value by removing black color from s. But due to p acquiring black color, we could remove excess black from v.

The second subcase arises when p is black. In this case, we cannot readjust excess black. But the excess black is transferred to p. So, the issue of excess black is pushed one level up the tree. Figure below illustrates both subcases.

Case 3c: Final case we need to consider is when sibling s is red.

The case is illustrated in the following figure.

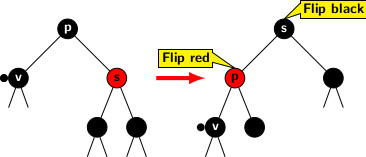
First restructure the case into one of previous cases where sibling of node with double black is black. We apply a left rotation around s. It brings s to position of p, and p is pushed down one level below. The color is flipped between the sibling s and the parent p. Now sibling of double black node v is black. Hence one of the previous cases applies.

We have discussed the deletion process by specifying general rules for handling extra black acquired by a node after deletion. So, it is time to examine some examples to familiarize the reader with actual operations. In the next blog we will deal with examples.

Back to Index