Insertion Sort

Insertion sort is similar to how we sort the playing cards in a hand of a bridge game. The process of sorting a hand is as follows:

• Assume that cards in hand are already sorted,
• Pick a new card from the distributed pile,
• Check its appropriate place among the card already in hand,
• Create a slot for inserting the new card by sliding higher denomination cards to the right.

When sorting an array of elements, we assume that the elements are divided into two parts, viz., sorted part and unsorted part. The unsorted elements occur to the right of sorted elements. Initially, only the first element is considered sorted. The process is as follows:

• Pick the leftmost element of the unsorted part, save it as gap element,
• Compare gap beginning with the right-most sorted element,
• Shift the sort elements to the right until gap continues to be smaller,
• Now place gap element at the current place of sorted part of the array.

The figure below illustrates the insertion sort algorithm.

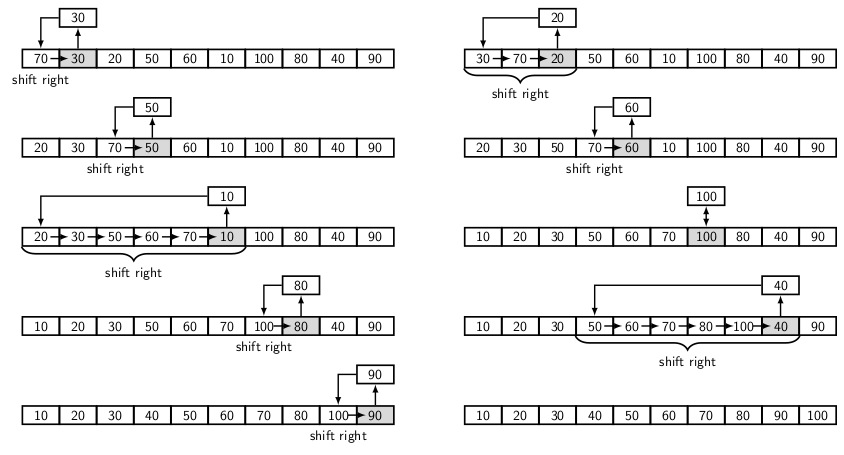
The critical point in insertion sort is data movement. If there is no data movement, then the list is sorted. A pair of loops control it. The first loop picks the next unsorted element from the list. The second loop controls the data movement, comparing the picked element with each sorted element one by one, beginning from the right.

• Initially, only the leftmost element of the array is sorted
• Remaining n-1 elements to the right is unsorted.

Since we have to pick one element at a time from the left of the unsorted part, the first loop runs n-1 times. The second loop scans all elements of the sorted part to create a slot where the next unsorted element can be slipped. Since, worst case size of sorted elements is n-1, the second loop may run for n-1 times. Therefore, the worst-case running time of insertion sort is O(n²).

The algorithm is as follows:

procedure insertionSort(int a[n]) {
  int  i, j, n, gap;

  for(i = 1; i < n; i++) {
        gap = a[i]; // Save the next unsorted element
        j = i-1;    // Compare and shift starting with rightmost sorted element
        while(j >= 0 && a[j] > gap) {
            a[j+1] = a[j]; // Shift elements to right to create slot 
            j--;
        }
        a[j+1] = gap; // Slot for new element
  } 
 
  return;
}

C Program for Insertion Sort

Back to Index