Heap Sort
Heapsort is a comparison-based algorithm. It allows the selection of the minimum element in O(1) time after the heap is built. However, deletion of the minimum spoils the heap property. So, after deletion, we must perform the heapify operation to restore the heap property for the remaining element. Heapify operation takes O(log n) time. Therefore, the running time of heapsort is O(nlog n). We have studied binary heaps in connection with priority queues. To refresh our memory, let us reexamine building a heap from a set of given elements from an ordered set.
Heap property
A heap is a complete binary tree such that the value stored in the node is smaller than or equal to that stored at any of its children nodes.
The following tree represents a binary heap.
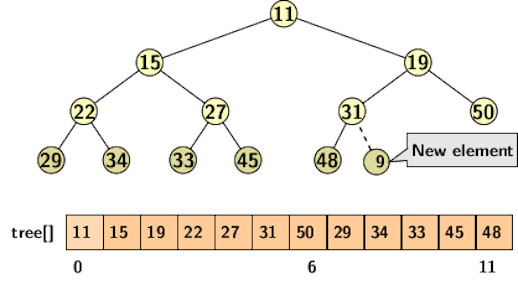
The parent of a node at position i is available in the index postion ⌉i⌈-1.
Building heap
Building a heap is simple. We take one element at a time and build the heap by applying a bottom-up heapify operation. The first element defines a heap of one element. Suppose a heap of a few elements is already available. The new element joins the heap at the leftmost vacant position in the highest level of the binary tree. It ensures the structural property of the heap remains unchanged. After creating a new node for an incoming element, we apply a bottom-up heapify operation along the tree path from the new node bottom up, sometimes known as shift up. It takes time of O(log n) to restore the heap property along the path.
Time complexity
The reader may come to a quick conclusion that the build heap has a worst-case running time of O(nlog n). However, the bound is not tight. We can compute a tight bound by observing that shift up operation requires time of O(h) where h is the height of the tree. The height increase gradually from 0 to log n. Since the heap is stored as a complete binary tree, we add nodes level-wise. All nodes of a height h require O(h) time for heapify. In a level h there can be at most ⌉n/2h+1⌈ nodes.
For example, a complete binary tree of 15 nodes has
- The number of node at height 3 is ⌉15/23+1⌈ = 1
- The number of node at height 2 is ⌉15/22+1⌈ = 2
- The number of node at height 1 is ⌉15/21+1⌈ = 4
- The number of node at height 0 is ⌉15/22+1⌈ = 8
Hence, the building heap requires a time of 15 units, the same as the number of nodes in a heap.
Let us check if the heap can indeed be built in O(n) time. Since we add nodes level-wise, and there are ⌉n/2h+1⌈ nodes per level, the time for building heap is:
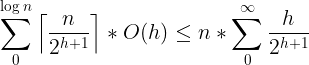
The final step of simplifying the RHS of the above equation is explained as follows. We know
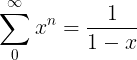
Differentiation of both sides of the above equation gives us
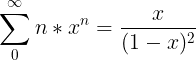
We substitute x = 1/2 to obtain:
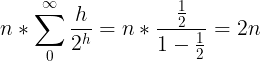
Therefore, the building of a heap of size O(n) requires linear time.
Sorting using heaps
Once the heap is available, we can repeatedly use deleteMin operations to select the minimum and append the deleted element to the sorted list. It produces a sorted list in time of O(n log n). Therefore, the time complexity for the heap sort is O(n + n log n) or O(n log n).