Hash Functions

Hashing uses a hash function to map a key (element) to an index position in the hash table. The function should have the following characteristics:

Low cost implies the hash function should be computable in time of O(1). Uniformity means the hash function should distribute the keys equally likely in its range space or the index space of the hash table. A hash function is deterministic if it gives the same hash value for a given input. If the hash function is not deterministic, it might give different index values in different operations. So, we cannot access a key from the stored slot.

The well-known hash functions use the following four methods:

The division method is the simplest and most well-used hashing function. It is given by:

h(x) = x mod m, where m is the hash table size.

Let us analyze the characteristics of the division function and its impact on different table sizes m. First, consider the value of m = 2p, then the division function will map any key x only to its lower order p bits. Therefore, a table size with a power of 2 is a bad choice, irrespective of key space. The division function maps all values of x = am + b map to the same table slot b. Therefore, choosing a prime value for m may not work out.

Let us find out the conditions for which the division function may work. We assume the base of the number system to be b such that b ≡ 1 (mod m). Now consider a key value of the form

$$k \mod m = \left(\sum_0^{r-1} k_i b^i\right) \mod m $$

Since \(b \equiv 1\mod m\), we can replace it by \((qm+1)\). So, the RHS expression of the above equation becomes

$$k \mod m = \left(\sum_0^{r-1} k_i (qm+1)\right) \mod m = \sum_0^{r-1} k_i \mod m$$

Hence, base values \(b = 2\) or \(b = 10\) are not good for the division hash function. The overall analysis points to the the fact that the division algorithm is bad.

The next function is known as the multiplication function. It relies on finding the product of key k by a randomly chosen fraction between 0 and 1 and extracting the middle bits of the product. Let us view the multiplication process of a value by a fraction in binary. The figure below depicts the long-hand process of multiplication.

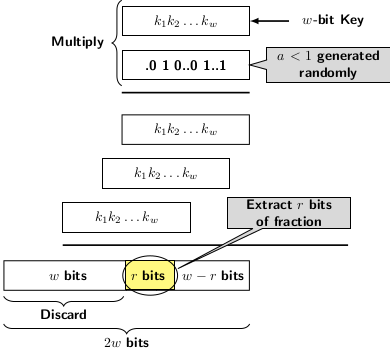
So, if we take \(r\) MSBs from the LSB of the product, the extracted value depends on the product. The mathematical expression of the multiplication function is:

$$\lfloor m.(k.a \mod 1)\rfloor$$

The value \(k.a \mod 1\) gives the fractional part of the \(w\) LSBs of the product. This value multiplied by \(m\) gives the table slot.

Let us examine some examples to determine how multiplication function spreads the hash values. Let \(m = 100\) and \(a = 1/3\)

According to Knuth a good choice for \(a = \left(\sqrt{5}-1\right)/2\).

A comparison of two hash functions: division and multiplication, is provided in the table below. It shows that the multiplicative function distributes the keys more evenly. Division function leads to more collisions.

Key \(\lfloor m*(k*a\mod 1)\rfloor\) \(k\mod m\)
123456 4 456
123459 858 459
123459 725 496
123956 21 956
129456 208 456
193456 383 456
923456 195 456

Midsquare and folding hash functions are quite simple. The mid-square function first squares the given key value, extracts a sequence of \(r\) middle digits from the result, and treats it as the hash value. Then extracted value depends on most digits as it is extracted from the middle of the product \(k*k\).

Folding divides the digits of the key \(k\) into \(p\) parts \(k_1k_2k_3\ldots k_p\) where each part except the last is of equal length. We add these parts and ignore the last carry. For example, assume that we have a table size = 100, and keys are 5678, 345, and 568901. Let us divide each key into parts of length 2 each. Then parts of 5678 are 56 and 78. Adding the two parts, we get 134. After ignoring the last carry 1, we get the hash value 34. Similarly, the hash of the other two numbers are:

There are other possibilities for designing hash functions. We described only a few well-known functions. We leave it to the readers to explore more functions.

In the next blog, we plan to discuss hashing methods..

Back to Index