Hashing by Chaining

A simple, uniform hash function spreads a set of random keys so that each key is equally likely to be hashed in any table slot. Let $P(k)$ be the probability of $k$ being hashed into a table slot. Distributiveness of the hash means each slot $j = 0, 1, \ldots, m-1$ to be occupied equally likely.

$$\sum_{k|h(k) = j} P(k) = \frac{1}{m}$$

In hashing by separate chaining, collision resolution is simple. All keys that map to the same table slot are chained together in a linked list. The hash table slots contain pointers to these linked lists. In other words, the hash table is an array of pointers of size $m$. The expected length of each linked list is $\frac{n}{m}$ which is known as load factor and denoted by $\alpha$. The hashing by chaining can be viewed as follows:

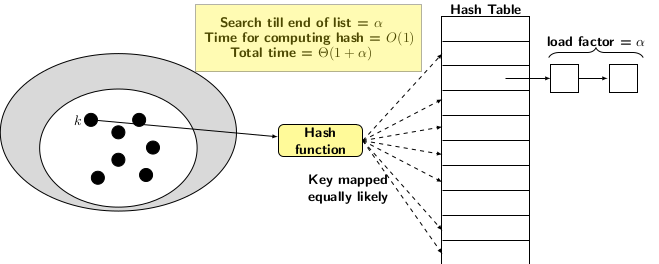
A lookup or search for an element in the hash table requires two steps:

Compute the hash value of the element
Index the table using the hash value to reach the linked list and search it for the element.

For the analysis of time complexity, we have to consider two cases:

Time for a successful search
Time for an unsuccessful search

Analysis of time complexity for unsuccessful search is easy with the assumption that the hash function is simple and uniform. An element may belong to any of the $m$ chains. As explained earlier, the length of any
chains or the linked list is $n/m = \alpha$. The average time to search for an element in a linked list of length $\alpha$ is $\alpha/2$. Since the searching also involves computing the hash value for the table index before searching the corresponding linked list, the time for an unsuccessful search is $(1+\alpha/2)$.

The analysis for time complexity for a successful search is a bit involved. We need to visualize the insertions as it happens into different chains. The first part of the analysis, of course, is to assume that the hashing function is simple and uniform. So, while inserting any element, we may hit any table slot equally likely. However, after that, we append the incoming element to the corresponding list. The expected length of the list to which the element $i$ gets inserted is $(i-1)/m$.

To calculate the complexity of the unsuccessful search, we need to find the average of all insertions to the hash table. The expression for the above is:

$$\begin{split} \frac{1}{n}\sum_{1}^{n} (1+\frac{i-1}{m}) & = 1 + \frac{1}{mn}\sum_{1}^n (i-1)\\ & = 1 + \frac{n(n-1)}{2m.n}\\ & = 1 + \frac{n-1}{2m}\\ & = 1 + \alpha/2 - \frac{1}{2m} \end{split}$$

Therefore, the average time complexity of an unsuccessful search is (1 + $\alpha/2$)

Hashing by separate chaining does not require much complex programming. We have already learned about programming with linked lists. The computations concerning hash functions are pretty simple. we provide some coding hints below. We create hash table as an array of linked nodes. Each node has two fields: $data$ and $next$. So, we can store the elements mapping to same hash value as a chain.

// We define a hash table of size 10.
// Modifying TABLE_SIZE, one can create a bigger table.

#define TABLE_SIZE 10
typedef struct node {
     int data;
     struct node *next;
} HTNODE;


// Create function creates and initializes the table of pointers
HTNODE ** createHT() {
    HTNODE ** head;

    head = (HTNODE **) malloc(sizeof(HTNODE *)*TABLE_SIZE);
    for (int i = 0; i < TABLE_SIZE; i++) {
        head[i] = NULL;
    }
    return head;
}

// We have used division hash function which may be replaced
int hashVal(int x) {
    return x % TABLE_SIZE;
}

The next two functions are for insert and search. Both use division function to find hash values. So all numbers ending with digit $d$ get mapped to same table slot and form a linked list. For navigating chain we have used a local pointer variable $c$.

// Insert function needs key value to be inserted
void insert(HTNODE ** head, int key) {
    int i;
    HTNODE * c;

    i = hashVal(key);
    HTNODE * newnode = (HTNODE *)malloc(sizeof(HTNODE));
    newnode->data = key;
    newnode->next = NULL;
    if(head[i] == NULL)
       head[i] = newnode;
    else {
       c = head[i];
       while(c->next != NULL) {
           c = c->next;
       }
       c->next = newnode;
    }
}

void search(HTNODE ** head) {
    int key,index;
    HTNODE * c;

    printf("Enter the element to be searched: ");
    scanf("%d",&key);

    index=key%TABLE_SIZE;
    if(head[index] == NULL)
         printf("Search element not found!");
    else {
         for(c=head[index];c!=NULL;c=c->next) {
             if(c->data == key) {
                 printf("Search element found!");
                 break;
             }
         }
         if(c==NULL)
             printf("Search element not found!");
     }
}

Delete function is similar to search. First, we need to locate the key to be deleted then apply deletion operation. However, to keep the program simple, delete is provided as a separate standalone function.

void delete(HTNODE **head) {
    int key, index;
    HTNODE *c;
    HTNODE *prev;

    printf("Enter the element to be deleted: ");
    scanf("%d",&key);

    index = hashVal(key);
    if(head[index] == NULL)
         printf("Element does not exist, deletion not possible!");
    else {
         if (head[index]->data == key) {
             // Case 1: deletion of the first element in the list
             head[index] = head[index]->next;
             return;
         } else {
             // Case 2: deletion of other elements in the list 
             prev = head[index];
             for(c=head[index]->next;c!=NULL;c=c->next) {
                  if(c->data == key) 
                      prev->next = c->next; // Delete the located element
                  else 
                      prev = c; // Continue search
             }
         }
         if(c==NULL)
             printf("Search element not found!");
     }
}

In the next blog, we will discuss hashing with open addressing.

Back to Index