Depth-First Search of a Graph
Graph search is a fundamental step in processing a graph. The search is a systematic traversal of the edges and visits of vertices. The search should ensure that no vertex is visited more than its degree times. However, the search should traverse each edge at least once. The two requirement leads to the conclusion that a graph search is a systematic way to ensure an edge is traversed at least once and at most a constant number of times (preferably ≤ 2).
Tremaux believed it is possible to systematically trace out a path in a maze from the available routes. His solution is to unroll a ball of thread from the entrance to the exit. He employed to avoid every threaded route that led to a dead-end. It helped him to avoid all explored paths. So, he was able to find the exit. We construct an equivalent graph of a maze by associating a vertex with each intersection and joining every pair of vertices by an edge if their corresponding intersections are directly reachable. An example of a maze and its equivalent graph is given below. The diagram is from Chapter 4 of Rober Sedgewick and Kevin Wayne’s text on algorithms.

Figure 1: Maze as a graph. (Source: Robert Sedgewick and Kevin Wayne, Chapter 4).
Tremaux’s graph exploration method was simplified later by Robert Tarjan. Tarjan noticed that the fundamental idea is to go as much deep as possible using unexplored edges. After reaching a point where no new vertex could be reached, backtrack and repeat the exploration of the remaining graph via the first unexplored edge. Continue the graph exploration until all edges have been traversed and all vertices are visited at least once. Tarjan named it as Depth-First Search (DFS). DFS traverses each edge twice and visits each vertex at most twice the degree times.
Tarjan’s DFS algorithm appears below.
// Initializations
initialization() {
index = 0;
for all ( v in V ) {
mark v "new"
T = {} // Initialize tree edges to empty set
while (there exists a "new" vertex v in V) {
DFS(v); // Perform DFS
}
}
DFS(v) {
mark v "old";
dfn[v] = ++index; // DFS numbers
for all (w in Adj(v)) {
if (w is "new") {
T = T + {(v,w)}; // Update T to include edge (v,w)
DFS(w); // Recursive call
}
}
}
The DFS number is sometimes referred to as pre-order because it is assigned to a vertex when it is marked “old.” We may choose to assign the numbering when DFS finally withdraws or backtracks from a vertex. That is when no unexplored edges exist at the vertex. The numbering is known as the postorder number or the reverse DFS number. We will discuss some interesting properties involving DFS and reverse DFS numbers later.
Before moving further, let us look at an example appearing in Figure 2.
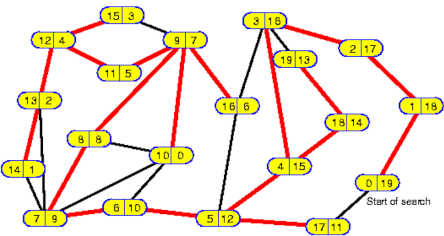
Figure 2: DFS and reverse DFS numbering (Source: unnamed Internet document).
The tree edges are color-coded by red, and the non-tree edges are color-coded by blue. Every vertex has a pair of numbers. The first number is the DFS number, and the second is the reverse DFS number of the vertex. The graph has 20 vertices. For a connected graph like that in the example, DFS generates a spanning tree. The tree is called DFS spanning tree or simply a DFS tree. The tree edges are those edges that lead to a new vertex during DFS. A non-tree edge leads to a previously discovered vertex (old vertex). In other words, a non-tree edge joins a pair of vertices not related by ancestor- descendant relations in the DFS tree.
The DFS and the reverse DFS numbers of a vertex v also represent the start and the finish time of DFS at v. The difference between the two numbers is equal to the number of descendant v in the DFS tree. For example, the vertex with a start time of 4 has its finish time of 15. It implies that vertex 4 has 11 descendants in the DFS tree, i.e., the subtree rooted at vertex 4 has 12 vertices, including itself.
DFS start and finish times: The difference between DFS finish and the DFS start time of a vertex v gives the number of descendants of v in the DFS spanning tree.