Graph Properties and Computer Representation
Let us discuss some well known properties of an undirected graph before exploring the ways to process a graph.
Graph property-1: An undirected graph has even number of vertices of odd degrees.
The proof of the above property is simple. If we add the degrees of all vertices then
Σ deg[v] mod 2 = 0 (the sum is an even number, why?)
But summing of degrees of all even degree vertices gives an even number. It implies that the sum of degrees of all odd degree vertices must also be an even number. It implies that there can be only even number of odd degree vertices.
Graph property-2: Let G be a graph with n vertices and assume that the degree of each vertex is at least ⌈(n-1)/2⌉ then the graph is connected.
Let n=2k, for k=1, 2, …. Let G be disjoint union of two complete subgraphs both having k vertices. Then the degree of each vertex in G is at least k-1. However G is disconnected. So to have G connected the minimum vertex degree should be k.
Now consider the case when G has 2k-1 vertices. Again let G be disjoint union of two complete subgraphs, one having k and other having k-1 vertices. The minimum vertex degee required for this to be true is k-2. So, the minimum vertex degree required for G to be connected is k-1.
Combining the two cases the minimum vertex degree required for G to be connected is:
- n/2 when n is even, and
- (n-1)/2 when n is odd.
The two conditions for connectivity can be expressed together as ⌈(n-1)/2⌉
Graph property-3: A connected graph with n vertices has at least n-1 edges.
Let G have 1 vertex. It is obviously connected. So, the property holds. Now let G be a graph with n ≥ 2 vertices. Choose an arbitrary vertex v from G. Consider the subgraph H = G - {v}. H may consist of k connected components Zi. Assume that Zi has ni vertices. By the induction hypothesis each Zi has at least ni-1 edges. The total number of vertices in subgraphs is equal to
Σi (ni) = n-1
We can continue the discussion on more graph properties. But our focus is graph algorithms. So we stop the discussion on graph properties for the moment. Let us focus on the computer processing of graphs. The first and foremost question is: how to represent a graph as abstract datatype?
A graph essentially represents relationships between objects or things. We can use a matrix to capture relationships between objects. Therefore, the standard form for computer representation of a graph with n vertices is a matrix of size n2. An entry
a[i, j] = 1 if there is edge (i, j) ∈ E
a[i, j] = 0 otherwise
In other words, the ijth entry is 1 if the object i is related to the object j. In the pictorial representation, we denote the relationship by an edge joining the related objects. A 0 entry indicates the absence of an edge. The matrix is called the adjacency matrix because it represents the relationship if a vertex is adjacent to another. Figure 1 illustrates the adjacency matrix representation.
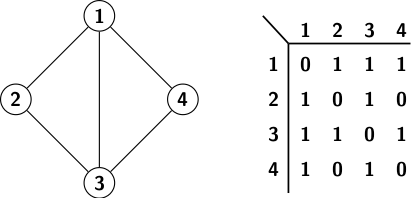
Processing a graph requires every entry of the adjacency matrix to be accessed. So any graph algorithm requires time of at least O(n2).
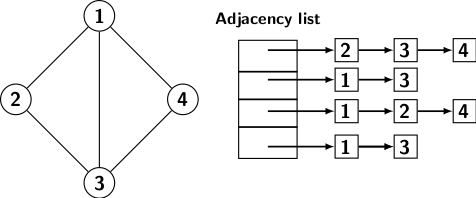
However, if the graph is sparse, then most entries of the adjacency matrix are zero. So, representing graphs using a matrix is expensive. We can use a representation that lists the edges incident at every vertex. The adjacency list representation of a graph consists of n lists, one corresponding to each vertex. Every edge is listed twice in such a representation. Adjacency list representation of the graph in Figure 1 is given below.