Implementation of Graphs in C
The next thing we address is that of graph implementation in C. For a graph, we have three items vertices, edges, and weights associated with edges. We have not discussed weighted graphs. Weighted graphs represent transportation networks, computer networks, and other purposes where edge weight quantifies the efforts needed for going from one vertex to another. Weighted graphs may be directed or undirected. An example of a weighted graph is shown in the picture below.
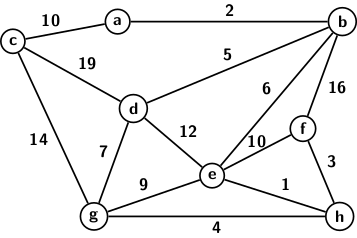
The graph may be assumed to represent the distances between cities, where nodes are cities, and edge labels are distances between cities it connects. The same graph may also represent a computer network. The nodes are for computers, and edges are for links between the pair of computers it connects. An edge label denoting the RTT in milliseconds between the computers at the end vertices. One can think of such weighted graphs as a pipeline network representing quantities of the flow of oil or water or gas flow between end vertices of edges. So, weighted graphs have a lot of applications. The most important problem one would like to solve in weighted graphs is the shortest path. We will return to the shortest path problem sometime later in the blog.
Having discussed weighted graphs, let us examine the implementation issues. We assume graphs as static structures unless specified otherwise. So, a graph can be specified by
- Adjacency lists
- A list of edges
- Adjacency matrix
When a graph is specified as a list of edges, we should first convert the graph to its adjacency list or adjacency matrix representation. Because in most applications, we process the graph from its adjacency list representation.
We assume the graph is specified by edges (pair of end vertices) and the corresponding labels. The structure for the implementation of graphs must be able to store three things, pair of end vertices and the edge label. The first end vertices are considered the source, and the other is the destination. To represent the vertices, we require a data type NODE. It stores the destination of an edge from the current node. An array of node pointers defines the entire graph structure. More specifically, head[i] denotes the adjacency list of node i for i = 0, 1, 2, …. The adjacency list of a vertex i is created by linking alldestination vertices of edges with source i. So, the data type NODE and GRAPH as specified as follows.
typedef struct node {
int dest; // Denotes the end vertex with which current vertex is connected
int weight;
struct node* next;
} NODE;
typedef struct graph {
// An array of pointers to represent adjacency lists
NODE* head[N];
} GRAPH;
After specifying the GRAPH type, we have to create a graph from the input set of edges. The function createGraph given below can create a directed, or an undirected or a weighted graph. We specify the graph type by the user’s input ‘d’, ‘u,’ or ‘w.’ The input is accepted from the function main(). createGraph() takes a flag value for creating the type of graph that the user wants. We store edge labels in a separate field within the node structure. However, it may not be used for graph processing unless needed for an application. The rest of the function is self-explanatory.
GRAPH* createGraph(EDGE edges[], int n, int flag) {
// Allocate storage for the graph data structure
GRAPH* graph = (GRAPH*)malloc(sizeof(GRAPH));
// Initialize head for all vertices
for (int i = 0; i < N; i++) {
graph->head[i] = NULL;
}
// Add edges to the directed graph one by one
for (int i = 0; i < n; i++) {
// Get the source and destination
int src = edges[i].src;
int dest = edges[i].dest;
int weight = edges[i].weight;
// Allocate a new node of adjacency list from src to dest
NODE* newNode = (NODE*)malloc(sizeof(NODE));
newNode->dest = dest;
newNode->weight = weight; // Save the edge weight
// Point new node to the current head
newNode->next = graph->head[src];
// Point head to the new node
graph->head[src] = newNode;
// Allocate a new node of adjacency list from `dest` to `src`
// for undirected graph
if (flag==0) {
newNode = (NODE*)malloc(sizeof(NODE));
newNode->dest = src;
newNode->weight = weight;
// Point new node to the current head
newNode->next = graph->head[dest];
// Change head to point to the new node
graph->head[dest] = newNode;
}
}
return graph;
}
The only other important function is to print the adjacency lists. The print function is quite straightforward. We wrote one print functions for all three graphs. For weighted graphs, we also print edge weights along with adjacency list. We use an indicator flag w for the same. The print function appears below.
// Prints adjacency lists of a graph
void printGraph(GRAPH* graph, int w) {
for (int i = 0; i < N; i++) {
// Prints the current vertex its neighbors
NODE* ptr = graph->head[i];
if (!w) {
// Print unweighted graph
while (ptr != NULL) {
printf("(%d —> %d)\t", i, ptr->dest);
ptr = ptr->next;
}
} else {
// Print weighted graph
while (ptr != NULL) {
printf("%d —> %d (%d)\t", i, ptr->dest, ptr->weight);
ptr = ptr->next;
}
}
printf("\n");
}
}