B-Tree Deletion Operation

Suppose we want to delete a key k from a node n. If n is not in a leaf, we can replace k with the largest key k1 in the left subtree under node n. The key k1 would occur in a leaf node L. The deletion process is essentially a generalization of the deletion of a key in BST. Therefore, all deletions occur in leaf nodes. It may lead to an underflow. An underflow occurs when the number of keys in a leaf node is less than M/2. If the sibling node has extra keys to share, keys can be moved to the deficient node and restore the requirement of the B-Tree. However, if the sibling has just M/2 keys, we have to merge the two siblings into one node. Merging may percolate up and require merging at a level up. If children of the root merge to form one node, a new root is created, decreasing the height by 1. Thus repeated deletions may lead to a reduction in tree height.

deleteKey(k, r) {
    (n, i) = BtreeSearchKey(r, k); // Locate the node and the key position
    if(!isLeaf(n)) {
         // n is an internal node
         removeKey(n, i);
         
         // Find the smallest key k1 greater than k  
         // k1 is guaranteed to be on a leaf node L
         (L, j) = BtreeLocateLargerKey(n,i); 
         
         // Copy L.key[j] in position n.key[i]
         L.key[j] = n.key[i]; 
         
         // Delete L.key[j]
         removeKey(L, j); 
    } else {
        // n is a leaf node 
        if(isUnderflow(n)) {
             m = n.sibling;
             borrow_cum_merge(m, n);
        }
    }
}

borrow_cum_merge(m, n) {
      // m is the sibling of n;
      if( isRich(m)){ 
          // A key can be borrow from m
          borrow a key from m via the parent node p;
      } else{ 
          // m is 1 key away from underflowing 
          // Pull the key from the parent ’p’, and merge it
          // with the keys of ’n’ and ’m’ into a new node
          mergeNodes(n, m); 
          if( isUnderflow(p)) {
              // Recursively call borrow_cum_merge 
              u = p.sibling;
              borrow_cum_merge(u, p);
          }
     }
}

A few points in the pseudo code for borrow_cum_merge() need a bit of explanation.

• The function removeKey() may require data movement inside L.
• Te functions isRich() and isUnderflow() just require checking of key count in a node.

The function isRich returns TRUE if count is greater than M/2. On the other hand, isUnderflow returns TRUE if count is less than M/2. Therefore, isUnderflow() and isRich() can be implemented using one single function.

If an underflow occurs after the deletion from a node, then a key can be borrowed from its rich sibling. However, it the sibling itself is one key away from underflow, then we perform a merging of keys as follows:

• Pull the key from the parent whose right pointer points to the sibling node.
• Merge the key retrieved from the parent, the remaining keys from node of the deleted key, and the keys from the sibling.

The merging process reduces the number of children of the parent by one while the sibling becomes richer by addition of left out keys from the deleted node, and the key pulled out from the parent node.

It is time to examine a few examples of deletions in a B-Tree. Let us begin with the most simple example, i.e., the deletion of a key from a leaf node. We need to consider three different possibilities in deleting key from a leaf node L.

• The simplest possibility is when L has more than M/2 keys.
• The second possibility occurs if L has exactly M/2 Keys, but the sibling of L has surplus keys.
• The third possibility occurs if both L and its sibling have exactly M/2.

The first possibility is handled as shown in the figure below.

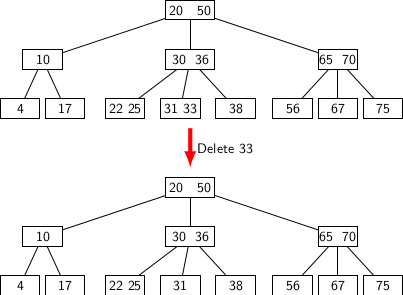
Deleting 33 from the leaf node having keys {31, 33} has no effect overall configuration of B-Tree as one key is still left in that leaf.

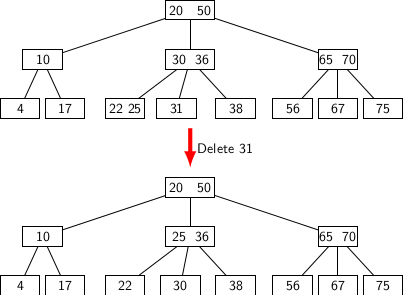
The next figure illustrates the second possibility. Deletion of the key 31 leads to the elimination of the leaf containing it. However, the left sibling of the concernied leaf has keys {22, 25}. Therefore, we can borrow one key from the sibling via the parent node. It leads to replacing 31 by the spare key 30 from the parent, while the key 25 is promoted to the parent node. So, deletion of the key 31 only requires a rearrangement of keys among the leaf nodes and their parent.

The configuration of nodes describing the third possibility appears in the figure below. We attempt to remove key 30. The sibling of the leaf containing 30 does not have a spare key.

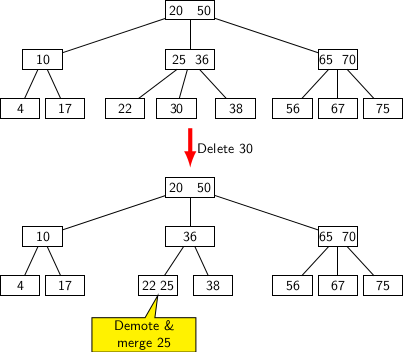
We may pull a key from the parent node to replace the node containing 30. However, it causes the parent to lose a child. Therefore, the number of child pointers from the parent is reduced by 1. We can handle it by pulling a key from the parent and merging it with one key in the relevant leaf node. So, 25 is pulled from the parent and merged with the leaf containing 22.

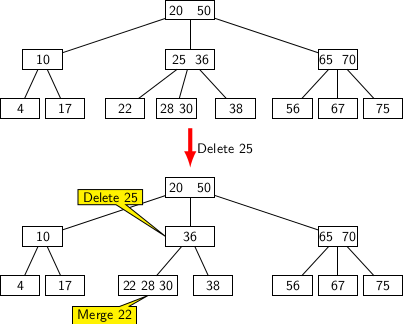
Considering all possible situations arising from the deletion of key from a leaf node, let us consider the situations that may arise in deletion operation from an internal node. Figure below illustrates one such situation. In this case, key 25 is deleted. But deletion results in the left leaf node being orphaned. So, we need to merge its keys with the non-full sibling node.

The second situation occurs when we attempt to delete a key from a node having M/2 keys. So the deletion leads to a node having less than the required number of keys. For example, suppose we want to delete key 36 from the tree given below.

We can merge its children and create a leaf node containing keys {30,38}. However, it leads to an unbalanced tree as leaf nodes are not at the same depth. How can we handle it? The simplest way is to pull up a key from the right child of the parent node. So, 70 goes to the parent node. The height of the tree is reduced by 1.

Back to Index