Bubble Sort

Bubble sort works on the principle of floating the lightest element to the top. We view the input as consisting of elements from a totally-ordered set. An element is heavier (lighter) than another if the former is greater (smaller) than the latter. Bubble sort makes the heavier elements sink to the bottom, and lighter elements float to the top. The figure below illustrates the first pass of the bubble sort algorithm.

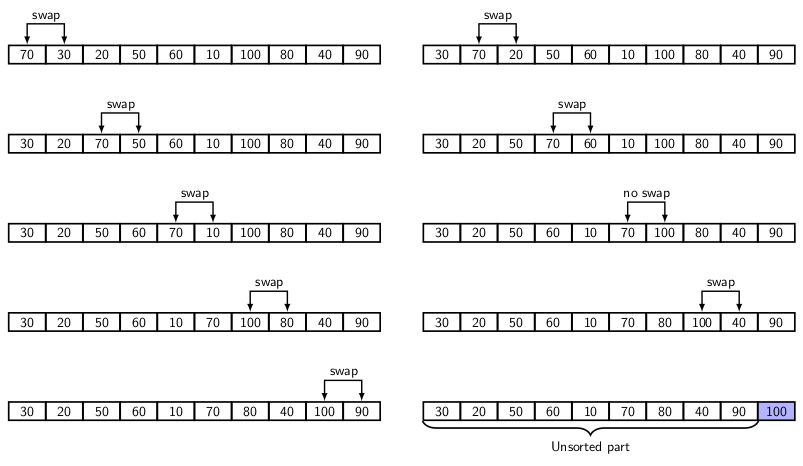
Figure 1

It is a swap-based algorithm. Starting with the leftmost end of the input list, it compares adjacent pairs of elements. If the heavier element is on top, then the two elements are swapped. After the first pass of n-1 compare-swap operations, the heaviest element occupies the bottom-most (nth) position of the list. Now the list consist of a unsorted part of n-1 elements and a sorted part of one element. The sorted part is excluded from the next pass of comparison. So, the unsorted list size is reduced to n-1. With every pass of compare-swap, the size of the sorted part increase by one. Therefore, with n-1 passes the size of the sorted part becomes n. The algorithm is given below.

 procedure bubbleSort(A) {
  n = A.length();
  do { 
    swapped = FALSE; // Flag used to indicate swaps
    for(i = 0; i < n; i++) {
      if (A[i] > A[i + 1]) { 
        swap(A[i], A[i + 1]); // Exchanges A[i] and A[i+1]
        swapped = TRUE;
      }
    }
    n--; // Size of unsorted part decreases
  } while(swapped)
}

Next, we deal with selection sort. It chooses the minimum of the remaining input sequence and places the element as the next element in sorted order. If we repeatedly execute the method starting with the input sequence of n elements, then a selection step reduces the input sequence by one each time. Therefore, with n-1 selection steps, we complete sorting of the input sequence. Since each selection step requires k, for k=n, n-1,…, 1 comparisons, the total number of comparisons is O(n²).

C Program for Bubble Sort

Back to Index