Binomial Trees

An interesting tree structure called a binomial tree is based on the concept of binomial coefficients. The definition of binomial trees relies on the recursive rules for the computing binomial coefficients. We define binomial trees using a base case and a recursive rule for the generation of higher-order binomial trees as follows:

Base case: A binomial tree order 0 has a single node.
Recursive rule: A binomial tree of order k is constructed by merging two binomial trees of order k-1, where the root of one tree becomes the left child of the root of the other.

Figure 1 illustrates a few binomial trees of small orders.

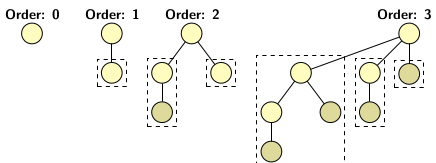
Figure 1

Let us explore some properties of binomial trees before discussing implementation issues. A binomial tree of order 0 has one node. Merging two binomial trees of order 0 creates one binomial tree of order 0. It has two nodes. Similarly, a binomial tree of order 2 has four nodes. In general a binomial tree of order k has 2^k nodes. We can verify the fact also from examples of binomial trees shown in Figure 1. More properties of binomial trees are as listed below:

The root of a binomial tree of order k has k children
The leftmost child of the root is the root of a binomial tree of order 0
The second leftmost child is the root of a binomial tree of order 1
In general i the leftmost child is the root of a binomial tree of order i

A forest of binomial trees defines a binomial heap. If the binomial heap has n nodes then it consists of binomial trees equal to the number of 1 bits in binary representation of n. For example, if n=13, the binomial heap representing it consists of three binomial trees B₃, B₂, and B₀ that correspond to 1 bits in binary representation of 13, i.e., 1101. Figure 2 illustrates the equivalence of heap and its binomial trees.

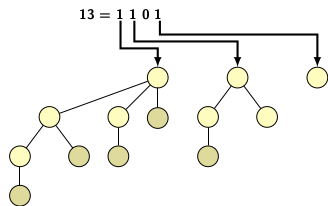
Figure 2

Merging two binomial forests is the fundamental operation in manipulating binomial heaps. We carry out joining from the lowest order to the highest order and stopping at the order where it ends up with a tree of non existent order. The process of merging is akin to the addition of two binary numbers. Figure 3 depicts binary addition in reverse order where carry bit corresponds to the generation of a new binomial tree in the merging process.

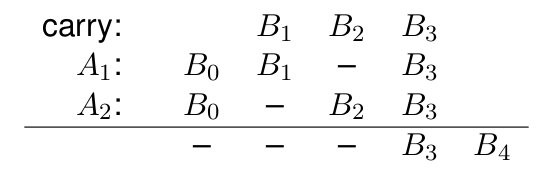
Figure 3

For example, consider merging of two binomial heaps H₁ and H₂.

H₁ consists of three trees B₀, B₁, B₃.
H₂ consists of three trees B₀, B₂, B₃.

As explained in Figure 3, we merge the binomial trees of the same orders belonging to two heaps starting with the lowest order trees. The merging process completes when no pair of binomial trees of the same order is left. A straightforward merging cannot maintain heap property. To maintain heap property, we choose the larger of the roots of the pair of trees a child of the smaller. In the first merging operation we choose a B₀ from H₁ and another from H₂. Merging these two trees, we get a new B₁. The result of the merging is shown in the right half of the figure below.

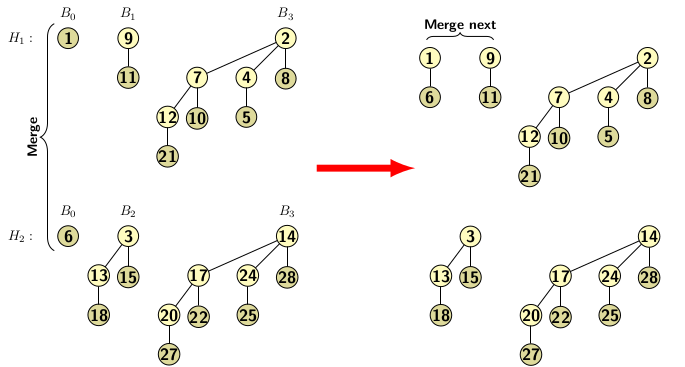
Figure 4a

Next, we take the B₁ from H₁ and merge it with the newly generated tree B₁. It produces a new B₂. The result is illustrated in Figure 4b.

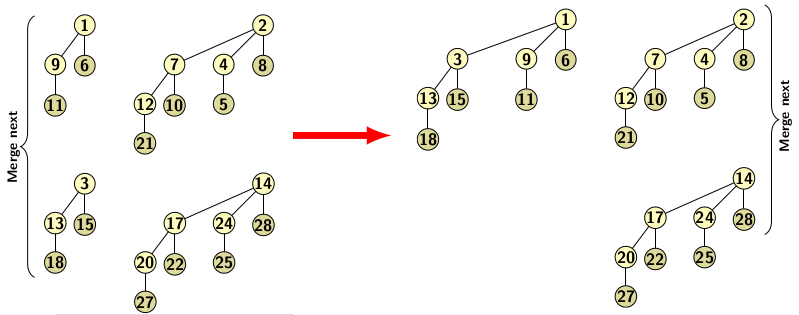
Figure 4b

So, in the third merging the new B₂ tree is merged with B₂ available in H₂. The merging creates a new binomial tree B₃. However, a binomial tree B₂ is left unmerged in heap H₂. Therefore, when merging completes, we are left with a heap consisting of two binomial trees B₂ and B₃ as shown in Figure 4c.

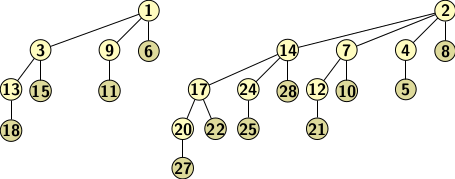
Figure 4c

Merging a pair of trees takes O(1) time. Two heaps together may consists of up to O(log n) trees, so the merging takes O(log n) in the worst-case. If we maintain the trees in the forest in sorted order according to heights, then the merging stop with the smallest non-existent tree. However, merge is performed most frequently. Therefore, a binomial forest maintained according to ascending order of the constiuent binomial trees. The key algorithm for merging is linking of two binomial trees. It is given below:

linkBinomialTrees(T, S) {
    r1 = getRoot(T);  // Root of the tree T
    r2 = getRoot(S);  // Root of the tree S
    if (r1->key < r2->key) { 
         // Since key in the root of S is smaller than key in the root of T
         // link the root of T as child of the root of S.         
         r2->parent = r1; 
         r1->child = r2; 
         r2->sibling = r1->child;
         r1->degree += 1;
     } else {  
         // Key in root of T is smaller, link S to T. 
         r1->parent = r2;
         r2->child = r1;
         r1->sibling = r2->child;
         r2->degree += 1;
     }
     return T;
}

Next blog will deal with operation on binomial heaps

Back to Index