Basic Properties of Binary Trees

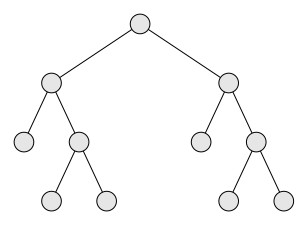
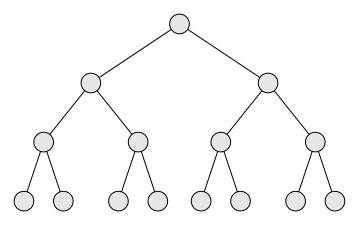
In this blog we focus on a few commonly used properties of binary trees. An internal nodes in a binary tree may have either one child or two children. A binary tree where each internal node has exactly two children is known as a strictly binary tree. If all the leaf nodes of a strictly binary tree is at the same level then we call such a binary tree as full binary tree. Figures below shows a strictly binary tree and a full binary tree.

**A strictly binary tree and a full binary tree**

Since each internal node may have two children, the maximum number of nodes at level i is 2ⁱ. It implies that maximum number nodes in a binary tree of height h is

$\sum_{i=0}^h 2^i = 2^{h+1}-1$

Sometimes, we may be interested to know the relationship between internal nodes and leaf nodes in a binary tree. Let:

The number of leaf nodes be:L,
The number of internal nodes be: I.

In a strictly binary tree the number of leaf nodes is equal to the number of its internal nodes plus 1, i.e., L = I+1. We can prove it by induction. Let the total number of nodes be N, for N=3, the only possible configuration for a stricly binary tree will be: a root and its two children.

So, the property stated above is valid. Let the property be true for any strictly tree of height h. Now consider a strictly binary tree T of height h+1. If we delete the root of T, then it falls apart as two strictly binary trees. Each of these subtrees T_L and T_R has a height less than h. Therefore, by induction the property must hold separately in each of the subtrees. So,

I(T_L)+1 = L(T_L)
I(T_R)+1 = L(T_R)

The number of leaf and internal nodes in the orignal tree are:

L(T) = L(T_L) + L(T_R), and
I(T) = I(T_L) + I(T_R) + 1

Now, we just combine the earlier two equations to conclude the fact that

L(T) = I(T) + 1

It is simple to observe that any chain of internal nodes can be collapsed to a single link. It implies, we can convert any binary tree into a strictly binary tree. Therefore, the relationship between leaf no L(T) is equal to one more than the number of nodes with two children.

The minimum height of a binary tree with N nodes is $h = \lceil 2^{\log N+1}\rceil-1.$ The formula can be easily proved using induction.

Back to Index