Maintaining a Balanced Binary Search Tree
The average case analysis of Binary Search Trees (BST) shows that any operation (search, insertion, deletion) on balanced BSTs requires a worst-case time of O(log n). Before proceeding further, let us formally define the balance property.
Balance Property: A BST possesses balance property if the difference between the heights of the left and the right subtrees of every node of the tree is 1, 0, or -1.
A leaf node has no left or right child. Therefore, the height difference between its left and the right subtree is 0. In other words, every leaf node of a binary tree possesses the balance property.
We cannot always depend on a nice random input distribution to expect that a BST to preserve balance property. As a BST undergoes a series of insertions and deletions, the balance property also gets disturbed. Furthermore, sometimes the initial sequence of insertions may generate a completely skewed BST as shown below.
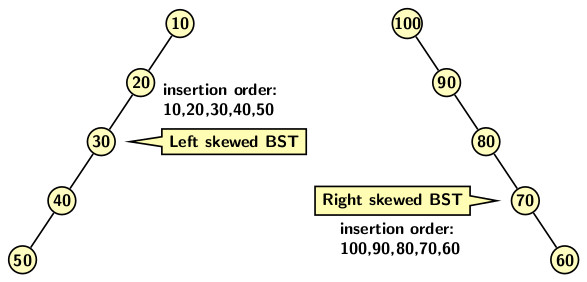
For achieving the worst-case time of O(log n) per operation on a BST, we should restore balance property every time tree becomes unbalanced. A BST may eventually become unbalanced as a sequence of insertions and deletions is applied over time. It implies that we need to address the following question.
- How the balance property be restored after a BST becomes unbalanced due to mutating operations?
We view an insertion or a deletion as a mutating operation because such an operation modifies the BST. However, a search is a non-mutating operation because it never alters a tree.
Adelson-Velsky and Landis (AVL) came up a recursive O(1) operation to balance a BST if it loses the balance property. The operation is known as a rotation. A rotation is required after an operation if a disbalance occurs at a node in the tree. AVL tree also requires each node to maintain height information along with other required information as needed for a BST node. We use the following minimal definition of an AVL tree node:
typedef struct Node {
int info, ht;
struct Node *left,*right;
} AVLNODE;
The height information will be used to find out the balance factor of each node. The balance factor of a node is the differnce between heights of its left and right child. The other normal operations of a BST apply to an AVL tree. However, we need to add additional features to a BST to maintain it as height balanced tree as mutating operation may often cause a disbalance at a node.
The operation which restores balance is known as rotation. A rotation involves a tri-node structure in a BST. The tri-node structure consists of
- A node where balance factore is disturbed,
- One of its child and
- One of its grandchild.
There rotation types depends on the pattern formed by a tri-node configuration mentioned above. We refer to the tri-node as a zig-zig or a zag-zag pattern, where a “zig” to refer to a left and a “zag” to refer to a right branch. So, if the child and grandchild of the node are left child of their respective parents then a zig-zig pattern is formed. Similarly, if the child and the grandchild of the node are right child of of their respective parent then a zag-zag pattern is formed.
There are two types of rotations:
- A single rotation
- A double rotation
A single rotation may either be a left or a right rotation, depending on the direction of rotation. The right rotation applies to the pattern where the imbalance at a node occurs due to a zig-zig pattern. More precisely, a zig-zig pattern relates to the imbalance occurring in the left subtree of the left child of a node. It also referred to as the case of an outside imbalance, because it happens due to the outer tree of the left child. The figure below illustrates the zig-zig tri-node configuration and the result of a single right rotation.
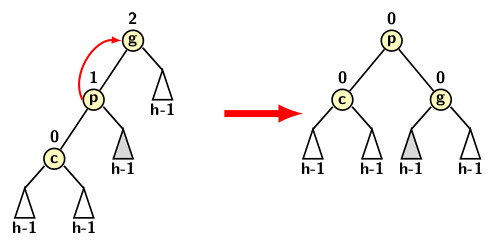
The right rotation operation preserves the BST property. It changes the root pointers of at most four subtrees, viz., T1, T2 of node c, T3 of p, T4 of node g respectively. T1 and T4 are outside trees and T2 and T3 are inside trees. From BST properties we know that T1 < c < T2 < p < T3 < g < T4, where Ti, for i=1,2,3, 4 refers to all key values in the subtree. After rotation, g becomes right child of p and T3 becomes left child of g. Since p < g, and T3, the rotation preserves the relative ordering of keys p, g, and in T3, i.e, p < T3 < g. The relative positions of T1, c and T4 are unchanged with respect to p. Therefore, the BST relationship is preserved after rotation. C-function for single right rotation is provided below.
AVLNODE *rotateRight(AVLNODE *g) {
// Tri-node forms a zig-zig pattern
AVLNODE *p = g->left; // p goes to top
AVLNODE *T2 = p->right; // g > p > T2
p->right = g; // p < g
g->left = T2; // T2 < g
g->ht = max(height(g->left), height(g->right)) + 1;
p->ht = max(height(p->left), height(p->right)) + 1;
return p;
}
On the other hand, if the tri-node configuration forms a zag-zag pattern, it implies that the balance factor of a node is disturbed due to right subtree of a node. It mirrors the zig-zig case and alternatively known as a subcase of outside imbalance because imbalance occurs due to outer tree of right child of a node. The ordering of keys in this case is T1 < g < T2 < p < T3 < c < T4. A single left rotation can restores the balance. We can also prove that rotation also preserves the BST property in a similar way as we did earlier in zig-zig case. Figure below illustrates a right rotation.
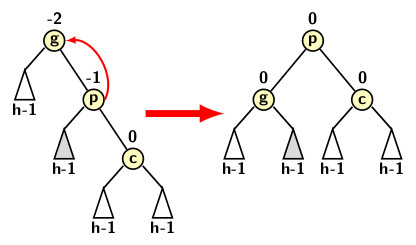
Single left rotation is given below. It is very much similar to single right rotation.
AVLNODE *rotateLeft(AVLNODE *g) {
// Tri-node forms a zag-zag pattern
AVLNODE *p = g->right; // y > x
AVLNODE *T2 = p->left; // x < T2 < y
p->left = g;
g->right = T2;
g->ht = max(height(g->left), height(g->right)) + 1;
p->ht = max(height(p->left), height(p->right)) + 1;
return p;
}
We have not specified two functions: max and height. The first one finds the maximum of two elements and the second one gets current height of the node from “ht” field.
The imbalance at a node may occur due to the right subtree of the left child of a node in a BST; we refer to the configuration of tri-node structure as zig-zag pattern. There is also a symmetric pattern of zag-zig where the tri-node structure consists of a node, its right child, and its left grandchild. Since the imbalances are due to inner trees, the two cases are sometimes considered as subcase of the inside imbalance case. A single rotation cannot fix the balance in the case of a zig-zag or zag-zig configuration. The figure below indicates that a single rotation only flips one configuration to the other.
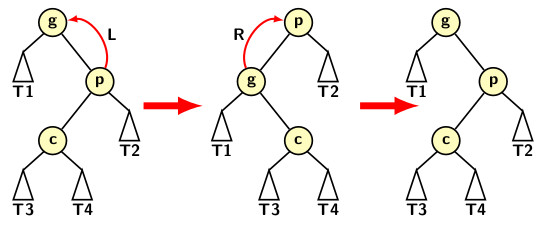
A double rotation consists of two rotations in sequence. It is either
- A single right followed by a single left rotation, or
- A single left followed by a single right rotation.
The two rotations types are shown in the figures below. In the first figure we consider the tri-node configuration forming a zig-zag pattern. The first rotation converts the tri-node configuration to zig-zig pattern. Then, one more single right rotation on zig-zig pattern can restore the balance factors of the node.
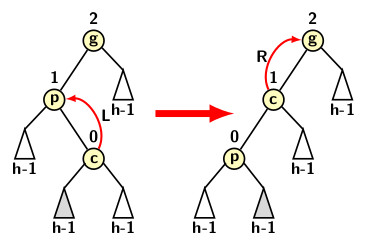
In contrast, a single right rotation on the zag-zig pattern converts it so zag-zag pattern. Now a single left rotation can restore the balance of the node.
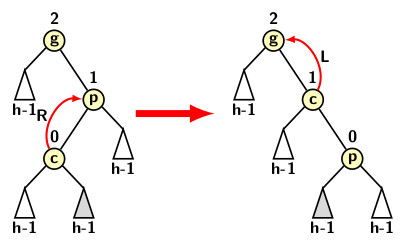
The functions for double rotations are simple. For zig-zag pattern, first the root of the right subtree should be rotated left. Following the left rotation a zag-zag pattern gets created that needs a right rotation to fix the imbalance. A symmetric situation occurs for a zag-zig pattern.
// Double rotate for zig-zag pattern of trinode configuration
AVLNODE *rotateLeftRight(AVLNODE *g) {
g->left = rotateLeft(g->left);
return rotateRight(g);
}
// Double rotate for zag-zig pattern of trinode configuration
AVLNODE *rotateRightLeft(AVLNODE *g) {
g->right = rotateRight(g->right);
return rotateLeft(g);
}
The question that remains unresloved is: where the rotation should be applied?
We end this blog here. We shall examine the case of height violation caused by a new insertion in an AVL tree the next blog.