Analysis of Quick Sort

Worst-case analysis

Worst-case behaviour occurs if excluding the partitioning elements, partition returns one array of size n - 1. The worst-case materializes when we have a sorted input. The cost of partitioning in this case is Θ(n). The recurrence relation for running time is:

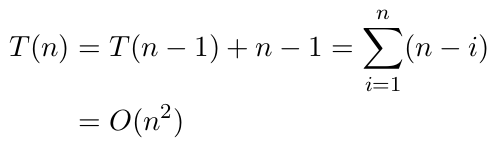
Average case analysis

Quick sort average case analysis is based on the following assumptions:

All permutation of the input sequence is equally likely,
The pivots used at all-recursive levels are random.

It implies some splits may be bad and others are good. So, by recursive partitioning, the bad splits are compensated by good splits. Let T(n) be the expected running time. For the boundary condition we have T(0) = T(1) = b, where b is some constant. Assume that the pivot is the ith element of the array. So, the split produces one partition of size i - 1 and the other of size n - i

Therefore, the recurrence formula for time complexity is:

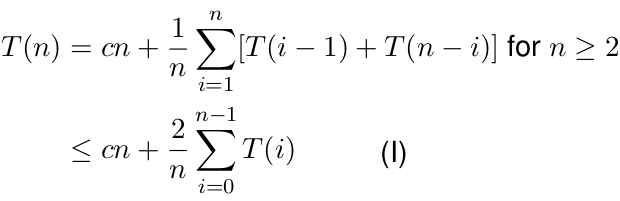
We want to prove that for n ≥2, T(n) ≤ k log_en, where k = 2c + 2b. Let us check the validity for n = 2.

T(2) = c.2 + T(01) + T(1). So, T(2) = 2b + 2c.

If we substitute n = 2 in the expression k log_en, then we get

k.2 log_e2 = 2k * 0.69173 .. > k = 2b + 2c.

Now we let n ≥ 2. The reformulate the inequality (I) as:

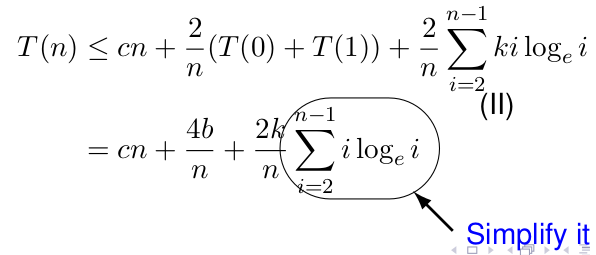
To simplify the summation in the above equation, from Figure 2, we observe that the function ilog_e i is concave upwards.

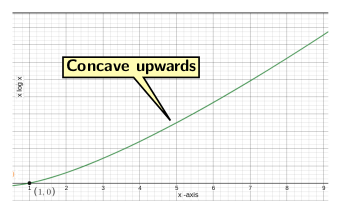
Figure 1: The function ilog_e i is concave upwards.

Therefore,

So, the overall expression for T(n) is now simplified as:

For n ≥ 2 and k = 2b + 2c,

Therefore, (A) < (B), i.e., (B) - (A) > 0 which implies:

Best case analysis

The best case occurs if the partition produces two equal subarrays, i.e., if the pivot is the median element. In this case, the partition sizes are:

one of size ⌊n/2⌋ and
another of size ⌉n/2⌈

The recurrence equation for time complexity is given by

Using T(1) = 0, 2^k = n, we get k = log n. Simplifying the above recurrence equation:

Balanced partitioning

The average case of quick sort is closer to the best case than the worst case. It is because balance of partitioning is reflected in recurrence for running time. Suppose the partitioning always produces 9-to-1 proportional split, then the recurrence relation will then be:

Figure 2: Cost of every level is cn up to depth log₁₀ n.

After depth log₁₀ n the cost becomes less than cn. So the expression cn log₁₀n dominates the cost. It implies that the balanced case is closer to the average case than the worst-case.

Back to Index